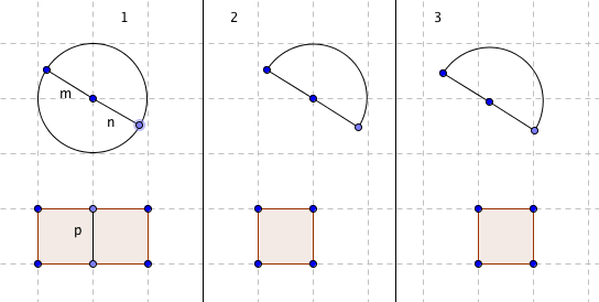
Book VII: Proposition 11 If a whole is to a whole as a subtracted number is to a subtracted number, then the remainder is to the remainder as the whole is to the whole.
In the picture above, I made my thinking and understanding of this proposition visual. In box 1 we have two wholes. They aren't equivalent wholes, but one is a whole circle and one is a whole rectangle. Now if we subtract the same amount from each whole, 1/2 (box 2), then the remainders in box 3 are equivalent in the sense that in proportion to their wholes, those two remainders are the same.
This is what I thought of the Euclid proposition and this is my own visual thinking and understanding.
In the picture above, I made my thinking and understanding of this proposition visual. In box 1 we have two wholes. They aren't equivalent wholes, but one is a whole circle and one is a whole rectangle. Now if we subtract the same amount from each whole, 1/2 (box 2), then the remainders in box 3 are equivalent in the sense that in proportion to their wholes, those two remainders are the same.
This is what I thought of the Euclid proposition and this is my own visual thinking and understanding.
 RSS Feed
RSS Feed