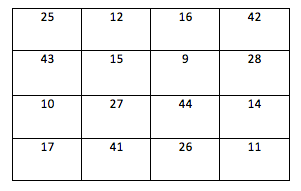
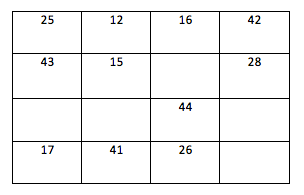
First I looked at the numbers in Ramanujan's square to see how some of the entries were related. I noticed that the entry in column 1 row 2 was the (entry in column 4 row 1) +1. So I did this in my magic square. I kept noticing patterns like this until I got to...
All the entries of the rows, columns, and diagonals add up to 95.
I thought this was an interesting exercise that made me wonder about how Ramanujan came up with this. Did he just play around with the numbers in his birthday until he got this result? Or had he been playing with simpler magic squares and decided to try his birthday?
In conclusion, I really enjoy these magic squares. Its solving a puzzle which is math but sometime people forget that solving puzzles or playing games is math too. This is definitely something I saw this semester that I will take into my classroom someday and show to students.





 RSS Feed
RSS Feed